Ta brskalnik ni podprt, zato nekatere funkcije ne bodo delovale.

Osnove Elektrodinamike

Osnove Elektrodinamike

Številski sistemi

Dvojiški (binarni) {0,1}
Desetiški (decimalni, dekadni) {0,1,2,3,4,5,6,7,8,9}
Osmiški (oktalni) {0,1,2,3,4,5,6,7}
Šestnajstiški (heksadecimalni) {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}

Desetiško v Dvojiško (10) → (2)

2  = 150  ostanek	0
2  = 75   ostanek	0
2   = 37   ostanek	1
2   = 18   ostanek	1
2   = 9    ostanek	0
2    = 4    ostanek	1
2    = 2    ostanek	0
2    = 1    ostanek	0
2    = 0    ostanek	1

300₍₁₀₎ = 100101100₍₂₎

Dvojiško v Desetiško (2) → (10)

100101100₍₂₎ =

Začneš s številko na desni, ki je $2^0$ , naslednja je $2^1$ , potem $2^3$ in tako naprej.

* 2^0  =  0 * 1    = 0
* 2^1  =  0 * 2    = 0
* 2^2  =  1 * 4    = 4
* 2^3  =  1 * 8    = 8
* 2^4  =  0 * 16   = 0
* 2^5  =  1 * 32   = 32
* 2^6  =  0 * 64   = 0
* 2^7  =  0 * 128  = 0
* 2^8  =  1 * 256  = 256

Na koncu samo sešteješ vse produkte.

100101100₍₂₎ = 300₍₁₀₎

Desetiško v Osmiško (10) → (8)

300₍₁₀₎ =

8 = 37   ostanek = 4
8  = 4    ostanek = 5
8   = 0    ostanek = 4

300₍₁₀₎ = 454₍₈₎

Osmiško v Desetiško (8) → (10)

454₍₈₎ =

  4 * 8^2 + 5 * 8^1 + 4 * 8^0 =
= 4 * 64  + 5 * 8   + 4 * 1   =
= 256 + 44 =
= 300

454₍₈₎ = 300₍₁₀₎

Desetiško v Šestnajstiško (10) → (16)

300₍₁₀₎ =

16 =  18 ostanek 12   = C
16  =  1  ostanek 2    = 2
16   =  0  ostanek 1    = 1

Rezultat se prebere od spodaj navzgor.

300₍₁₀₎ = 12C₍₁₆₎

Šestnajstiško v Desetiško (16) → (10)

12C₍₁₆₎ =

  1 * 16^2 + 2 * 16^1 + 12 * 16^0
= 256 + 32 + 12
= 300

12C₍₁₆₎ = 300₍₁₀₎

bonus: 16v2, 2v16, 2v8 in 8v2

Logične funkcije

Negacija

$x$	$y$
0	1
1	0

Konjunkcija

Druge možne notacije so z znakom & in ^.

$x_1 \phantom{a} x_2$	$x_1 \times{ x_2 }$
0 0	0
0 1	0
1 0	0
1 1	1

Disjunkcija

Druga možna notacija je z znakom ˅.

$x_1 \phantom{a} x_2$	$x_1 + x_2$
0 0	0
0 1	1
1 0	1
1 1	1

Zakonitosti

Zakon o zamenjavi

Zakon o združevanju

Zakon o združevanju 2

Zakon o razčlenjevanju

Teoremi

$x_1 \phantom{a} x_2$	$\overline{x_1} \phantom{a} \overline{x_2}$	$x_1 \cdot x_2$	$\overline{x_1}\cdot\overline{x_2}$	$\overline{x_1 \cdot x_2}$	$x_1 + x_2$	$\overline{x_1} + \overline{x_2}$	$\overline{x_1 + x_2}$
0 0	1 1	0	1	1	0	1	1
0 1	1 0	0	0	1	1	1	0
1 0	0 1	0	0	1	1	1	0
1 1	0 0	1	0	0	1	0	0

Četrti in osmi stolpec sta si enaka, tako kot tudi peti in sedmi stolpec.

Antivalenca

Ekskluzivna ALI vrata (EX-OR vrata)

slika EX-OR vrat

y = \overline{x_1} \cdot x_2 + x_1 \cdot \overline{x_2}

$x_1 \phantom{a} x_2$	$y$
0 0	0
0 1	1
1 0	1
1 1	0

Izhod je 1 takrat, ko sta na vhodih različni vrednosti.

$x_1 \phantom{a} x_2 \phantom{a} x_3$	$y$
0 0 0	0
0 0 1	1
0 1 0	1
0 1 1	0
1 0 0	1
1 0 1	0
1 1 0	0
1 1 1	1

Ko je liho število enic je y = 1.

Ekvivalenca

Ekskluzivna NE-ali vrata (EX-NOR gate)

slika vrat

y = \overline{x_1} \cdot \overline{x_2} + x_1 \cdot x_2

$x_1 \phantom{a} x_2$	$y$
0 0	1
0 1	0
1 0	0
1 1	1

Izhod je ena kadar sta vhodni vrednosti enaki.

$x_1 \phantom{a} x_2 \phantom{a} x_3$	$y$
0 0 0	0
0 0 1	1
0 1 0	1
0 1 1	0
1 0 0	1
1 0 1	0
1 1 0	0
1 1 1	1

Ta tabela je enaka kot EX-OR.

STIKALA

Delovno stikalo

delovno stikalo

Vklopi = tok teče skozi
Izklopi = ni toka

Mirovno stikalo

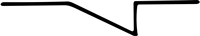
mirovno stikalo

Izklopi = tok teče skozi
Vklopi = ni toka

Menjalno stikalo

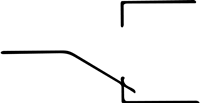
menjalno stikalo

Vklopi = tok po eni poti
Izklopi = tok po drugi poti

LOGIČNA VRATA S STIKALI

Negator

ALI vrata

IN vrata

NE-IN vrata

\overline{ x_1 \cdot x_2 } = \overline{x_1} + \overline{x_2}

NE-IN vrata

NE-ALI vrata

\overline{ x_1 + x_2 } = \overline{x_1} \cdot \overline{x_2}

NE-ALI vrata

EX-OR vrata

y = \overline{x_1} \cdot x_2 + x_1 \cdot \overline{x_2}

EX-OR vrata

EX-NOR vrata

y = \overline{x_1} \cdot \overline{x_2} + x_1 \cdot x_2

EX-NOR vrata

vaje realiziranja vezij

in risanja teh vezij v raznih

diagramskih stilih

LOGIČNA VEZJA

KOMBINACIJSKA VEZJA: Stanje izhoda je odvisno samo od trenutne kombinacije stanj vhodnih spremenljivk.
SEŠTEVALNIK: je vezje, ki tvori vsoto dveh binarnih števil
POLOVIČNI SEŠTEVALNIK: sešteje dve enomestni števili (binarni)

1171 words