Matematika

Linearna funkcija

$$\cdots$$

Kvadratna Funkcija

Je funkcija, ki jo lahko zapišemo z enačbo (splošne) oblike $f(x) = ax^2 + bx + c​$ kjer so koeficienti a, b in c poljubna realna števila in vodilni koeficient $a \neq 0​$.

Oblike kvadratne funkcije

Splošna: $f(x) = ax^2 + bx + c$

Temenska oblika: $f(x) = a(x - p)^2 + q$ . Števili p in q sta koordinati temena kvadratne funkcije. Teme je točka $\mathrm{T}(p, q)$ v kateri kvadratna funkcija doseže ekstremno vrednost. Za izračunati $p$ in $q$ lahko uporabimo naslednji formuli:

$$p = - \frac{b}{2a} \qquad q = \frac{4ac-b^2}{4a}$$

Ničelna oblika: $f(x) = a(x - x_1)(x - x_2)​$ . Števili $x_1​$ in $x_2​$ sta ničli kvadratne funkcije. V splošnem sta to kompleksni števili. Ničelno obliko lahko dobimo iz splošne z razcepom, lahko pa $x_1​$ in $x_2​$ izračunamo po naslednji formuli:

$$x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

Število, ki v zgornji formuli nastopa pod korenom, je diskriminanta kvadratne funkcije: $D = b^2 - 4ac$ . Diskriminanta nam pove, koliko realnih ničel ima kvadratna funkcija:

• Če je $D > 0​$, sta obe ničli kvadratne funkcije realni ($x_1, x_2 \in \mathbb{R}​$).
• Če je $D = 0​$, sta števili $x_1​$ in $x_2​$ enaki - kvadratna funkcija ima samo eno realno ničlo ($x_1 = x_2 \in \mathbb{R}​$).
• Če je $D < 0$, sta obe ničli kvadratne funkcije nerealni ($x_1, x_2 \notin \mathbb{R}$) - graf funkcije ne seka abscisne osi (v realnem koordinatnem sistemu.)

Graf kvadratne funkcije

Graf kvadratne funkcije narišemo postopoma:

• najprej narišemo graf $y = x^2$,
• potem ta graf raztegnemo z raztegom v smeri osi y za faktor $a​$
• nato ga še premaknemo s premikom za vektor ($p$, $q$)

Primer: $f(x) = 2x^2 - 12x + 16$

1. Najprej funkcijo preoblikujemo v temensko obliko: $f(x) = 2(x - 3)^2 - 2$
2. in potem narišemo:

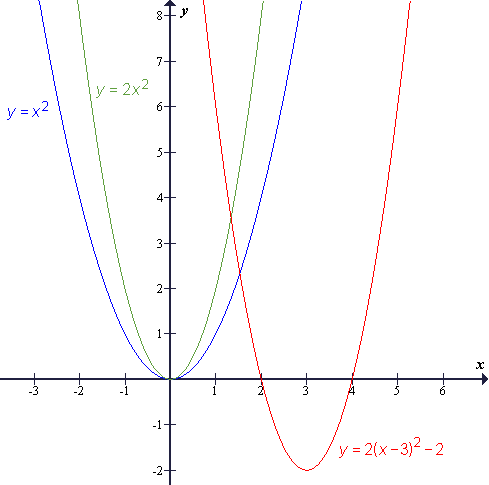
Iz zgornjega postopka vidimo, da vodilni koeficient a odloča o tem, kako je obrnjena kvadratna funkcija:

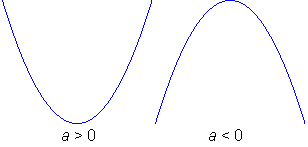
Racionalna funkcija

Racionalna funkcija je vsaka funkcija, ki jo lahko zapišemo z enačbo spodnje oblike, kjer je $p$ poljuben polinom, $q$ pa poljuben neničelni polinom.

$$f(x) = \frac{p(x)}{q(x)}$$

manjka se kr stvari

---

Polinomi

Splošni predpis polinoma stopnje n $(n \in \mathbb{N_0})$:

$$p(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \phantom{a}\cdots\phantom{a} a_2x^2 + a_1x + a_0$$

Trigonometrija

$$\cdots$$

Adicijski izreki

$$\sin 75^o \neq \sin 30^o + \sin 45^o \\[8pt] \sin 75^o = \sin (30^0 + 45^o)$$ $${\pm \pm} \quad \sin (\alpha \pm \beta) = \sin \alpha \cdot \cos \beta \pm \cos \alpha \cdot \sin \beta \\[8pt] {\pm \mp} \quad \cos (\alpha \pm \beta) = \cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta$$ $$\begin{array}{c|ccccc} \alpha & 0^o & 30^o & 45^o & 60^o & 90^o \\ \hline \sin \alpha & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1 \\ \cos \alpha & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 \end{array}$$

Zaporedja

Zaporedje je funkcija $f: \mathbb{N \to R}$

To pomeni, da poljubnemu naravnemu številu $n$ pripada določeno realno število, ki ga označimo $a_n​$ in ga imenujemo n-ti člen zaporedja.

Zaporedje ponavadi podamo s formulo za splošni člen.

Zgled: Zaporedje s splošnim členom $a_n = n^2 + 1​$ ima člene: $a_1 = 2​$, $a_2 = 5​$, $a_3 = 10​$, $a_4 = 17, \quad \dots​$

Lastnosti zaporedij

Zaporedje narašča, če za $an \in \mathbb{N}$ velja: $a_{n+1} > a_n$

Zaporedje pada, če za $an \in \mathbb{N}$ velja $a_{n+1} < a_n$

Zaporedje je omejeno navzgor, če obstaja realno število $M$, tako da za $an \in \mathbb{N}$ velja: $a_n \leqslant M$ . Število $M$ imenujemo zgornja meja zaporedja. Če je zaporedje navzgor omejeno, obstaja celo več zgornjih mej. Najmanjši med njimi pravimo natančna zgornja meja ali supremum zaporedja. Zaporedje lahko natančno zgornjo mejo doseže ali pa tudi ne. Če obstaja člen, ki je enak natančni zgornji meji, ga imenujemo maksimalni člen zaporedja.

Zaporedje je omejeno navzdol, če obstaja realno število $m$, tako da za $an \in \mathbb{N}$ velja: $a_n \geqslant m$ . Število $m​$ imenujemo spodnja meja zaporedja. Če je zaporedje navzdol omejeno, obstaja celo več spodnjih mej. Največji med njimi pravimo natančna spodnja meja ali infimum zaporedja. Zaporedje lahko natančno spodnjo mejo doseže ali pa tudi ne. Če obstaja člen, ki je enak natančni spodnji meji, ga imenujemo minimalni člen zaporedja.

Zaporedje je omejeno, če je navzgor in navzdol omejeno.

Vsota prvih n členov zaporedja

Poljubnemu zaporedju $a_n$ lahko priredimo zaporedje delnih vsot:

• $s_1 = a_1$
• $s_2 = a_1 + a_2​$
• $s_3 = a_1 + a_2 + a_3$

Oziroma na splošno: $s_n = a_1 + a_2 + \dots + a_n$

Število $s_n$ imenujemo n-ta delna vsota ali vsota prvih n členov zaporedja $a_n$. Drugo ime za $s_n$ je vsota končne vrste.

Aritmetično zaporedje

Aritmetično zaporedje je zaporedje, v katerem je razlika dveh zaporednih členov konstantna. To razliko označimo $d$ (diferenca).

Torej: $a_n - a_{n-1} = d$ oziroma: $a_n = a_{n-1} + d$ .

Formula za vsoto prvih $n$ členov aritmetičnega zaporedja (za vsoto končne aritmetične vrste):

$$s_n = \frac{n(a_1 + a_n)}{2}$$

Lastnosti aritmetičnega zaporedja:

• Če je diferenca $d > 0​$ (pozitivna), aritmetično zaporedje narašča.
• Če je diferenca $d < 0$ (negativna), aritmetično zaporedje pada.
• Če je diferenca $d = 0$, je aritmetično zaporedje konstantno.

Vsak člen aritmetičnega zaporedja (razen prvega) je enak aritmetični sredini svojih sosedov:

$$a_n = \frac{a_{n+1} + a_{n-1}}{2}$$

Geometrijsko zaporedje

Geometrijsko zaporedje je zaporedje, v katerem je količnik dveh zaporednih členov konstanten. Ta količnik označimo k ali q (kvocient).

Torej: $a_n / a_{n-1} = k$ oziroma: $a_n = a_{n-1} \cdot k​$

Formula za splošni člen geometrijskega zaporedja: $a_n = a_1 \cdot k^{n-1}$

Obrestni račun

Spremenljivka	Kaj pomeni
G - glavnica	Znesek, ki se nam obrestuje
o - obresti	Znesek, za kateregase glavnica poveča
p - obrestna mera	V %, banke računajo letno obrestno mero
r - obrestovalni faktor	$\mathrm{r} = 1 + \frac{p}{100}$
n - obrestovalna doba

Navadno obrestovanje

Glavnica ostaja enaka, obresti so enake.

$$o = \frac{G \cdot p}{100} \qquad o_n = \frac{G \cdot p \cdot n}{100} = \text{obresti po n letih}$$

Primer: Miha si od banke sposodi…

Obrestno obrestovanje

Glavnica se po računanju obresti veča, zato se tudi obresti s časom večajo.

$$G_0 = 1000 \\ G_1 = 1030 \\ G_2 = 1060,9 \\ G_3 = 1090,73$$

Odvod

Odvod funkcije $f(x)$ v točki $\mathrm{T}(x, y)$ je enak smernemu koeficientu tangente na graf te funkcije v tej točki. Označimo ga $f’(x)$. $f’(x_0) = k_t​$

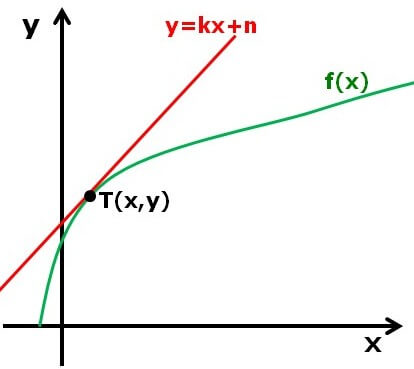
Pravila za odvajanje

• Produkt funkcije in konstante $\big(c \cdot f(x)\big)’ = c \cdot f’(x)$

• Vsota in razlika funkcij $\big( f(x) \pm g(x) \big)’ = f’(x) \pm g’(x)$

• Produkt funkcij $\big( f(x) \cdot g(x) \big)’ = f’(x) \cdot g(x) + f(x) \cdot g’(x)$

• Kvocient funkcij

$$\bigg( \frac{f(x)}{g(x)} \bigg)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g^2(x)}$$

Odvodi elementarnih funkcij

FUNKCIJA $f(x)$	ODVOD $f(x)’$
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	$\frac{1}{x}$
$log_ax$	$\frac{1}{xlna}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tanx$	$\frac{1}{cos^2x}$
$cotx$	$-\frac{1}{sin^2x}$

Kombinatorika

Kombinatorika je področje matematike, ki se ukvarja s tem, na koliko načinov je možno razporediti neko množico elementov ali na koliko načinov je možno izbrati elemente iz neke množice.

Kombinatorično drevo

S kombinatoričnim drevesom grafično prikažemo proces

Izbiranja odločitev. Drevo vseh možnosti narišemo tako, da vsako vozlišče razvejimo na toliko vozlišč, kolikor izbir imamo na voljo v danem koraku.

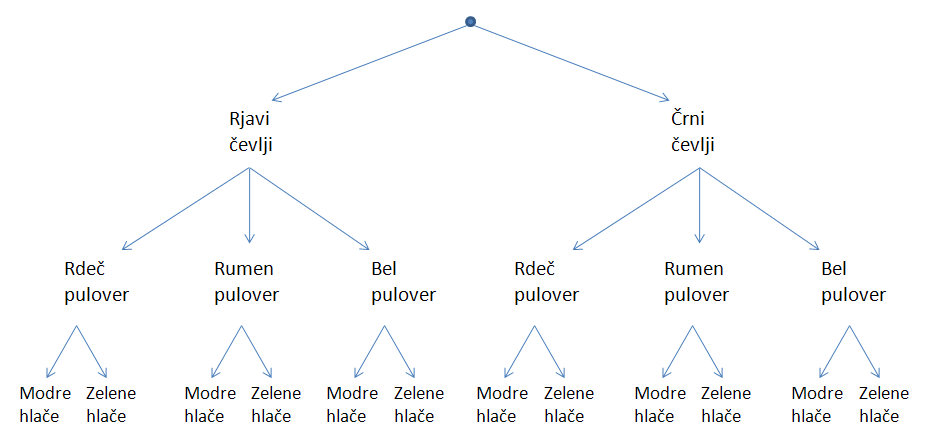
Pravilo produkta ali osnovni izrek kombinatorike: Če imamo na voljo m možnosti iz prve skupine in n možnosti iz druge skupine, izbrati pa želimo eno možnost iz prve in hkrati eno iz druge skupine, potem imamo na izbiro skupno m · n možnosti.

Primer: Pripravljamo darilo za rojstni dan. Najprej izberemo eno od daril (čokolada, igrača, knjiga, darilni bon), potem darilo zavijemo v eno od možnosti (škatla, darilna vrečka, darilni papir) in na koncu dodamo pentljo ene izmed barv (rdeča, modra, rumena). Koliko različnih daril imamo na voljo?

Rešitev: N = 4 · 3 · 3 = 36

Pravilo vsote: Če imamo na voljo m možnosti iz prve skupine in n možnosti iz druge skupine, izbrati pa želimo točno eno možnost iz prve ali iz druge skupine, potem imamo na izbiro skupaj m + n možnosti.

Primer: Na kosilo gremo lahko picerijo, ki ponuja 5 vrst pic, v mehiško restavracijo ki ponuja 3 vrste tortilj ali v italijansko restavracijo ki ponuja 4 vrste testenin. Koliko različnih kosilo imamo na voljo?

Rešitev: N = 5 + 3 + 4 = 12

Permutacije

Permutacije so razporeditve danih n elementov na n prostih mest. Če so vsi elementi med seboj različni, so to permutacije brez ponavljanja. Število permutacij brez ponavljanja izračunamo po formuli:

$$P_n = n \cdot (n - 1) \cdot (n - 2) \cdot … \cdot 3 \cdot 2 \cdot 1 = n!$$

To računsko operacijo imenujemo n fakulteta ali n faktorsko.

Primer: Koliko različnih petmestnih števil lahok zapišemo iz števk 1, 2, 3, 4, 5?

Rešitev: P₅ = 5! = 120

Variacije

Variacije brez ponavljanja so razporeditve n različnih elementov na r prostih mest. Pri tem je r < n, zato ostane nekaj elementov nerazporejenih. Število variacije brez ponavljanja izračunamo po formuli:

$$V^r_n = \frac{n!}{(n - r)!}$$

Primer: Koliko različnih trimestnih števil lahko sestaviš iz števk 1, 2, 3, 4, 5?

Rešitev: V³₅ = 5! : 3! = 20

Kombinacije

Če pri variacijah zanemarimo vrstni red in opazujemo samo, kateri elementi so izbrani, dobimo kombinacije. Kombinacije brez ponavljanja so izbire r (različnih) elementov izmen n različnih elementov, ki so na voljo. Število kombinacij brez ponavljanja izračunamo po formuli:

$$C^r_n = \frac{n!}{r! \cdot (n - r)!}$$

Izraz, ki nastopa na desni strani zgornje formule, lahko označimo tudi z binomskim simbolom:

$$\binom{n}{r} = C^r_n = \frac{n!}{r! \cdot (n - r)!}$$

Primer: Na koliko načinov lahko izberem iz razreda z 20 dijaki 3 predstavnike?

Rešitev: C³₂₀ = 20! / 3! · 17! = 1140

Verjetnost

Poskus je vsako hoteno dejanje, ki ga opravimo v natanko določenih pogojih.

Primeri:

1. Po mizi zakotalimo običajno igralno kocko.
2. Iz običajnega kompleta 32 kart izberemo eno karto.
3. Kupimo eno od 100 000 loterijskih srečk.

Predpostavimo, da se poskus vedno odvija pod enakimi, natančno določenimi pogoji. Pojav, ki se lahko v posameznem poskusu zgodi ali pa tudi ne, imenujemo dogodek.

Primeri:

1. Pade sodo število pik. Pade šestica. Padejo več kot štiri pike.
2. Izvlečena karta je as. Izvlečena karta je rdeče barve. Izvlečena karta je figura.
3. Kupljena srečka zadene glavni dobitek. Kupljena srečka zadene manjši dobitek. Kupljena srečka ne zadene ničesar.

Dogodke označujemo z velikimi tiskanimi črkami $A$, $B$, $C$, …

Dogodek je lahko:

• Gotov - ($A$ se zgodi pri vsaki ponovitvi poskusa): pri metu poštene igralne kocke pade manj kot 7 pik.
• Nemogoč - ($A$ se ne zgodi v nobeni ponovitvi poskusa): potegnemo belo kroglico iz posode, v kateri so samo črne kroglice.
• Slučajen - ($A$ se v nekaterih ponovitvah poskusa zgodi, v nekaterih pa ne, pri čemer pred posameznim poskusom ne moremo z gotovostjo napovedati, ali se bo zgodil): na loteriji z eno samo srečko zadenemo glavni dobitek.

Nasprotni dogodek $A’$ dogodka $A$ se zgodi, če se $A$ ne zgodi: Met igralne kocke $\rightarrow A$ - padejo več kot 4 pike; $A’$ - padejo največ 4 pike.

Verjetnost dogodka $A$ je enaka $P(A) = \frac{m}{n}$ , kjer je n-število vseh izidov in m-število ugodnih izidov.

Primeri:

1. Kolokšna je verjetnost dogodka $A$, da pri metu igralne kocke pade manj kot 5 pik?

Število vseh izidov : 6, število ugodnih izidov: 4. $P(A) = \frac{4}{6} = \frac{2}{3}​$

1. V besedi FIBONACCI na slepo prečrtamo eno črko. Kolikšna je verjetnost, da je prečrtana črka:
   • $A \qquad P(A) = \frac{1}{9}$
   • $C \qquad P(B) = \frac{2}{9}​$
   • samoglasnik $P(C) = \frac{1}{9}$